Problem Statement
A rectangle has one corner on the graph of y=16x², another at the origin, a third on the positive y-axis, and the fourth on the positive x-axis. If the area of the rectangle is a function of x, what value of x yields the largest area for the rectangle?
Process
|
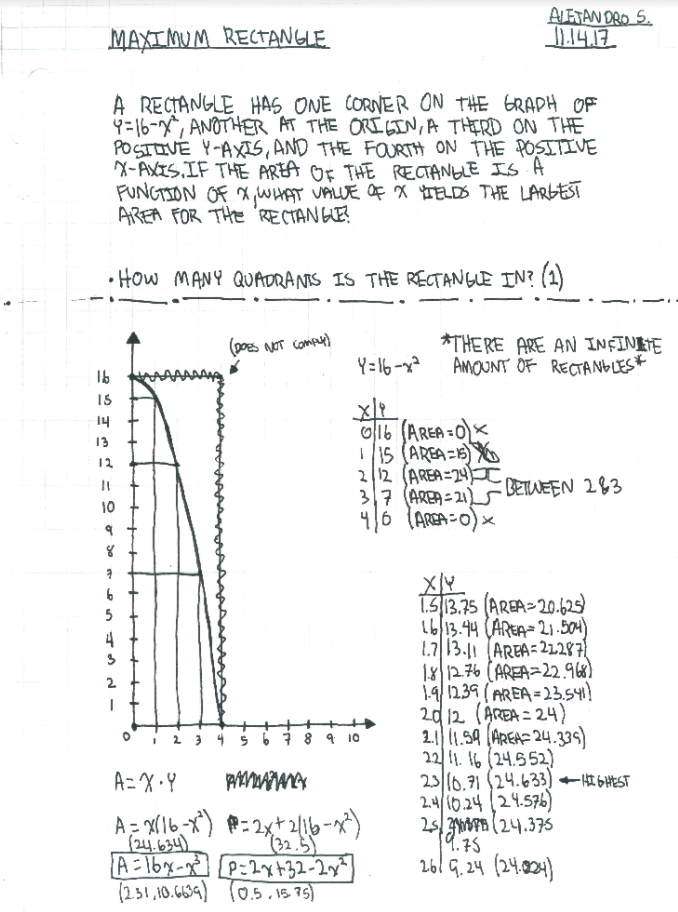
My initial attempt for this problem was to draw out the parabola y=16-x² which you can see I did in the middle of my paper (top-right). After my initial attempt at drawing the parabola, I thought that the maximum rectangle would be 64 (16 times 4), but I later found out that the rectangle had to be inside the parabola and not just outside where it's all nice and easy to do. You can also see that I initially drew a rectangle inside the graph but later scribbled it out because it did not comply with the problem statement. The function of Area is length times width but in our case it is x times y. So what I did is I did a t chart and started plugging and chugging and got higher and higher areas until I got bored and settled on 2.31. Now that I knew what was the highest area for a human to calculate without getting bored, I noticed since Area is x times y, we can plug y in. (A= x times y (16-x²). Now that we have the value for y, we can distribute the x into 16-x^2 and get, Area=16x-x³. I made sure that this equation was right and plugged in my x (2.31) and sure enough, I got the same area with the x and y values being 2.31 and 10.6639. Now that I had the area function down, all I needed was to do the perimeter function which was just as easy. Perimeter is 2l + 2w so instead of length and width, I did x and y. Now the function would be as follows, Perimeter= 2x + 2y, and we can plug in y so we can distribute and get the final function. P=2x+2(16-x²) -> P=2x+32-2x². I plugged this equation into Desmos and saw that the maximum area would be 32.5 and then found the x and y values (0.5, 15.75)
|
Solution
Maximum Perimeter:
To find the maximum perimeter, you first have to know the equation to find Perimeter. The equation for Perimeter is P=2l+2w. Now, in our case we had to plug in x and y so we just replaced l and w with x and y (P=2x+2y). Now that we have our adjusted Perimeter function, we can plug in our y (Y=16-x²), which would look something like this, P=2x+2(16-x²). Now that we have our y plugged in, we can distribute the 2 to the 16 and x² which would look like this, P=2x+32-2x². Now if you have Desmos you can plug in and get your maximum perimeter but in our class that was not our case. We had to plug and chug a lot to find the maximum perimeter using a t chart to find the maximum perimeter. Now if you did all that and found the x and y axis points (0.5, 15.75) that give you the maximum perimeter (32.5) you have successfully solved for perimeter.
Maximum Area:
To find the maximum area, you first have to know what the equation for finding area is. The equation for finding the area of a rectangle is (Area= length times width). We don´t have length and width with the rectangle that we´re given because we´re graphing it on the positive x and y axis. In that case, we´re going to need to switch up the formula to look like this, (Area= x times y). Now that we have our adjusted Area function, we can plug in the Y that was given to us in the problem statement, (Y=16-x²) so our equation should look something like this, A= x(16-x²). We can distribute the x to the 16 and the x² so our simplified equation would look like this,(A=16x-x³). Now that we have the equation, we can do a t chart and start plugging in numbers until we get the highest area for the rectangle. Once we got far enough with the numbers, my group and I came to the conclusion that the highest area would be 24.634 with the x axis being 2.31 and the y axis being 10.6639.
To find the maximum perimeter, you first have to know the equation to find Perimeter. The equation for Perimeter is P=2l+2w. Now, in our case we had to plug in x and y so we just replaced l and w with x and y (P=2x+2y). Now that we have our adjusted Perimeter function, we can plug in our y (Y=16-x²), which would look something like this, P=2x+2(16-x²). Now that we have our y plugged in, we can distribute the 2 to the 16 and x² which would look like this, P=2x+32-2x². Now if you have Desmos you can plug in and get your maximum perimeter but in our class that was not our case. We had to plug and chug a lot to find the maximum perimeter using a t chart to find the maximum perimeter. Now if you did all that and found the x and y axis points (0.5, 15.75) that give you the maximum perimeter (32.5) you have successfully solved for perimeter.
Maximum Area:
To find the maximum area, you first have to know what the equation for finding area is. The equation for finding the area of a rectangle is (Area= length times width). We don´t have length and width with the rectangle that we´re given because we´re graphing it on the positive x and y axis. In that case, we´re going to need to switch up the formula to look like this, (Area= x times y). Now that we have our adjusted Area function, we can plug in the Y that was given to us in the problem statement, (Y=16-x²) so our equation should look something like this, A= x(16-x²). We can distribute the x to the 16 and the x² so our simplified equation would look like this,(A=16x-x³). Now that we have the equation, we can do a t chart and start plugging in numbers until we get the highest area for the rectangle. Once we got far enough with the numbers, my group and I came to the conclusion that the highest area would be 24.634 with the x axis being 2.31 and the y axis being 10.6639.
Group Test/ Individual Test
|
Group Test:
For our group test, my group and I decided to have everyone understand the problem statement fully and also know every step of the way on finding the maximum area and perimeter. We also had alone work time where we would just plug numbers in and find areas and perimeters and later check on one another to see if we got the same answer. In the end, we got the area function right but we took too long and later found out that we didn't have enough time to do the perimeter and got it wrong because of it. Overall, I had an alright time doing the group test because half of the time was just work time and half of the other time was us actually talking. Individual Test: For my individual test, I did well on it only missing one point due to the fact that I messed up on the perimeter and didn't fully get all the way through with the maximum perimeter because of me being lazy and stopping at the x axis of 1.1 which got me the wrong perimeter. |
Evaluation/ Reflection
What really pushed my thinking was when Mr.Carter told us that you could use calculus to solve both the maximum area and perimeter and I wanted to learn it fast because he said it was the most efficient way of finding vertexes and in our case, the maximum perimeter and area. I got the most out of the overall work that had to go into the whole problem with plugging numbers in and just going and going higher forever. With that in mind, I would grade myself a nice A+ because I understood the problem and helped other people understand it as well.