For the past week or two, we have been working with Desmos to learn how to transform parabolas either up, down, left or right. We were given 5 activities to work on and each one challenged us differently. 

Process and Solutions

For our first activity (right), we had to predict if this guy could make the basketball shot by using parabolas. I took my time in predicting whether he would make it or not because in some shots, he would hit the rim and completely miss even when the parabola "said" he was going to make it.

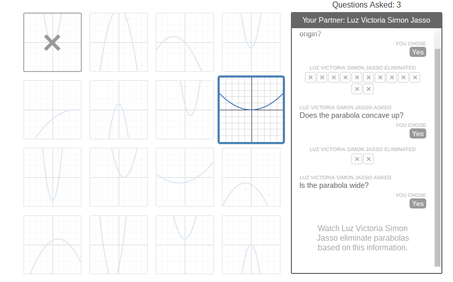
For our second activity (left), we did guess who but with parabolas. We had to use specific vocabulary like "vertex" or "origin" to pinpoint our partner's parabola they chose. For instance, when Luz asked, "Does the parabola concave up?", I immediately knew that she and I passed the game because there was one thing that distinguished my parabola over the other. Anyways, this activity taught me how to use the vocabulary of parabolas to "guess who?" anyone's parabola.

For our third activity (right), we learned vocabulary of the parabolas and also practiced sketching them. I put this picture to the right showing how the graph should be sketched with those requirements. 

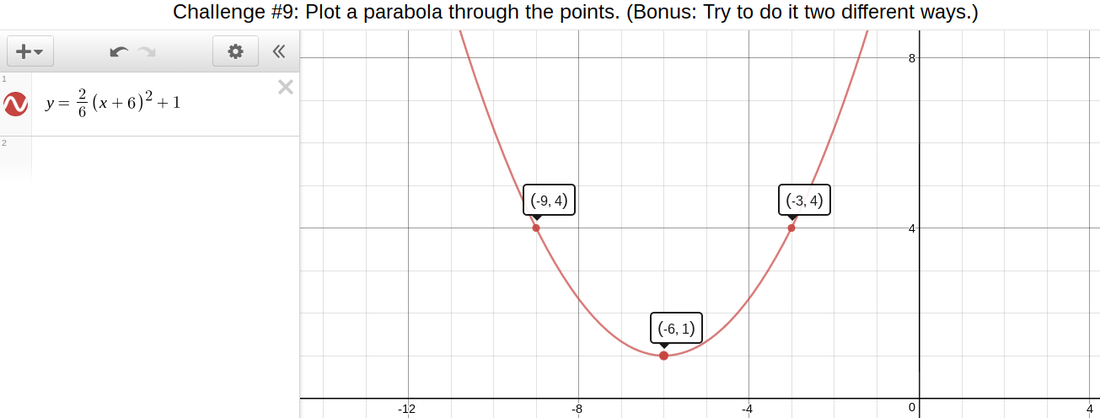
For our 4th activity (left), we had to manipulate parabolas to put them through specific points in the graph. For instance, the picture on the right shows how I used vertex form to make the parabola go left 6 and up 1. Then, I had to manipulate the parabola to make it go through specific points ((-9,4)(-3,4)). Anyways, this activity taught me how to use vertex form to make parabolas smaller/wider and where you should put them on the graph.

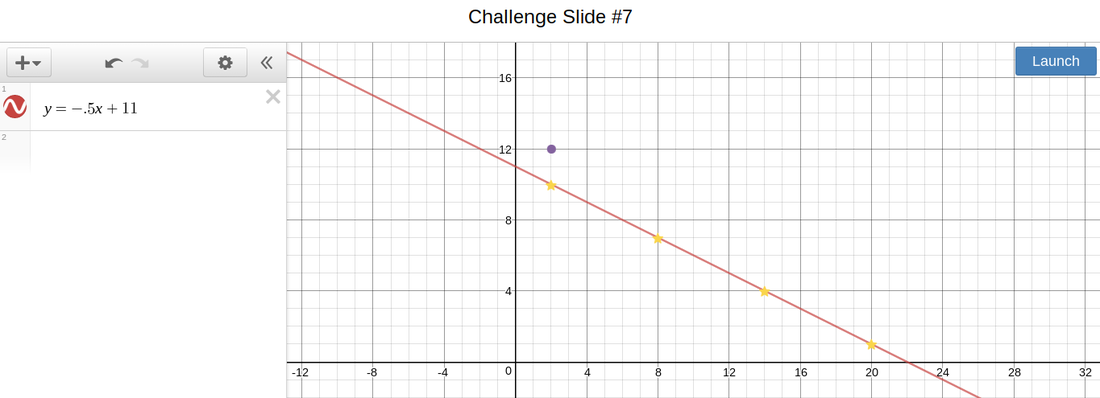
For our 5th activity (right), we did an activity called "Marble Slides". We had to manipulate parabolas to make them collect stars to pass the level. For instance the picture on the right, I had to collect 4 stars but I used a line segment because it would've been much easier for me to do it that way instead of a curvy parabola. Anyways, this activity taught me how to put parabolas through specific points.

What I Learned Throughout The Activities

• y= a (x-h)^2+k is the vertex form in which (h) tells you how far out to the right or left you go, When it is negative (-), the variable tells you to go (h) to the right and if it's positive (+), the variable tells you to to (h) to the left. So minus = goes to the 1st and 4th quadrant and positive = goes to the 2nd and 3rd quadrant. The variable (k) tells you to go up or down. If the variable is positive (+), you go up however much (k) is but if the variable is negative (-), you go down however much (k) is. The variable (a) tells you how wide or narrow the parabola is. For instance, if (a) was to be 10, you would have a very skinny parabola whereas if (a) was 1/10, you would have a very wide parabola. 
• While I was messing around with Desmos, I figured out how to make circles by accident! I forgot to put = between y and x (so y=x), and accidentally squared (^2) (x) and (y). The result was an equation that desmos couldn't compute so I typed this equation to make it so desmos could understand it: y^2+x^2=1 and it made a circle!​

Self Assessment:
Some learning goals I have for this semester are to grow as a teacher and be able to explain math better to other classmates. Other goals would be to start to learn calculus and learn some coding with it too. Aside from that, I'll keep growing in math everyday and I'll teach it to others as well.

Edits:
Enrique and Noah told me to make my pictures bigger so the text was readable.
Mr.Kirby told me to make a "Self Assessment" paragraph to explain my goals to others.