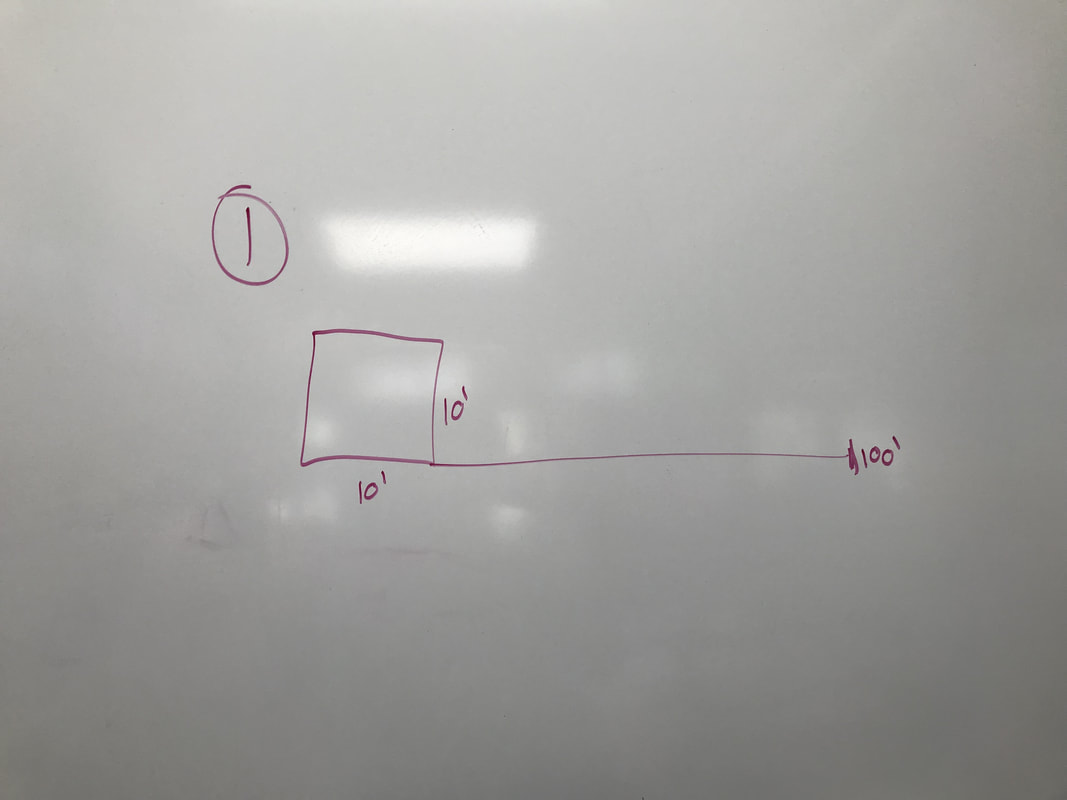Problem Statement
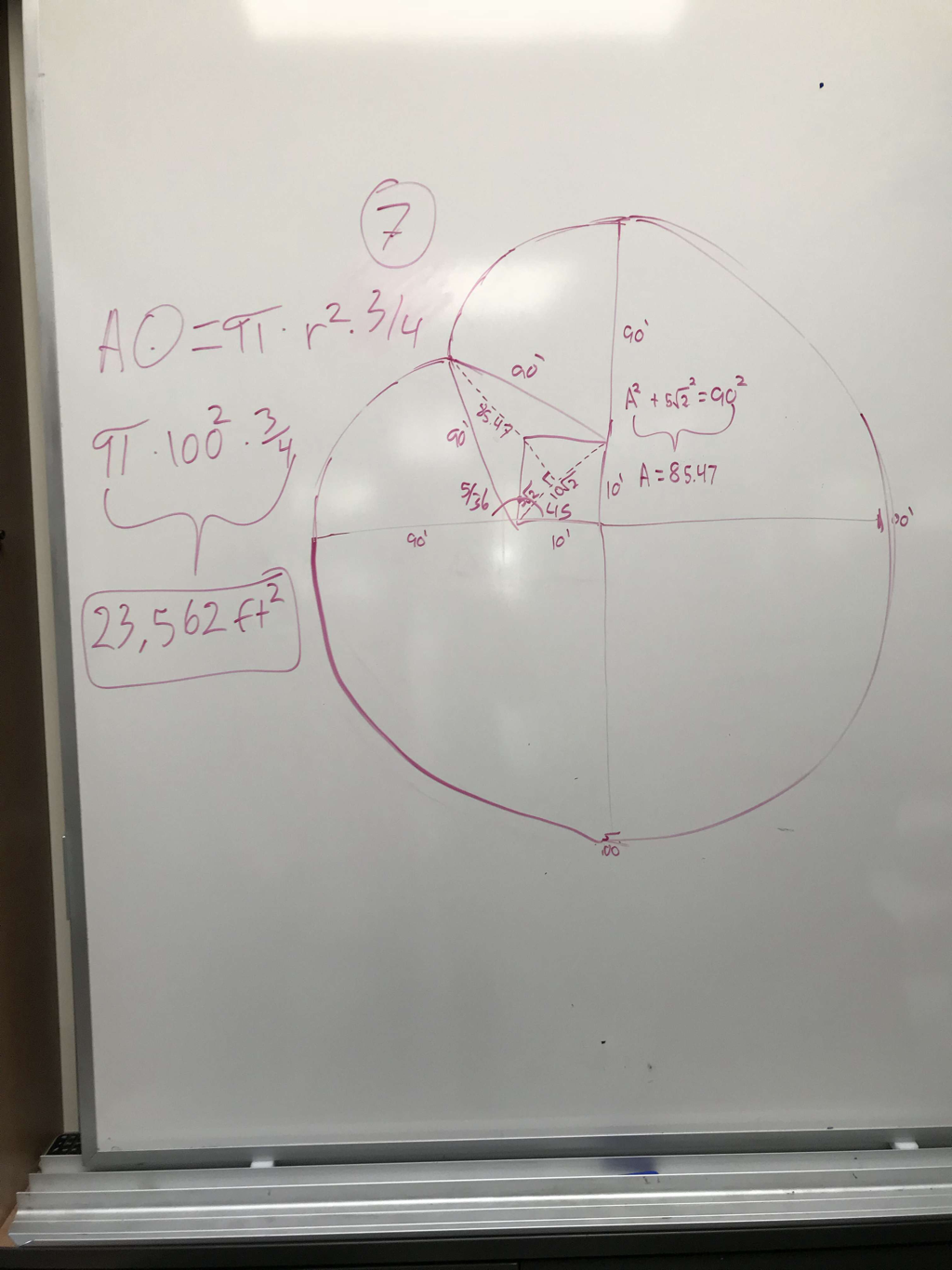
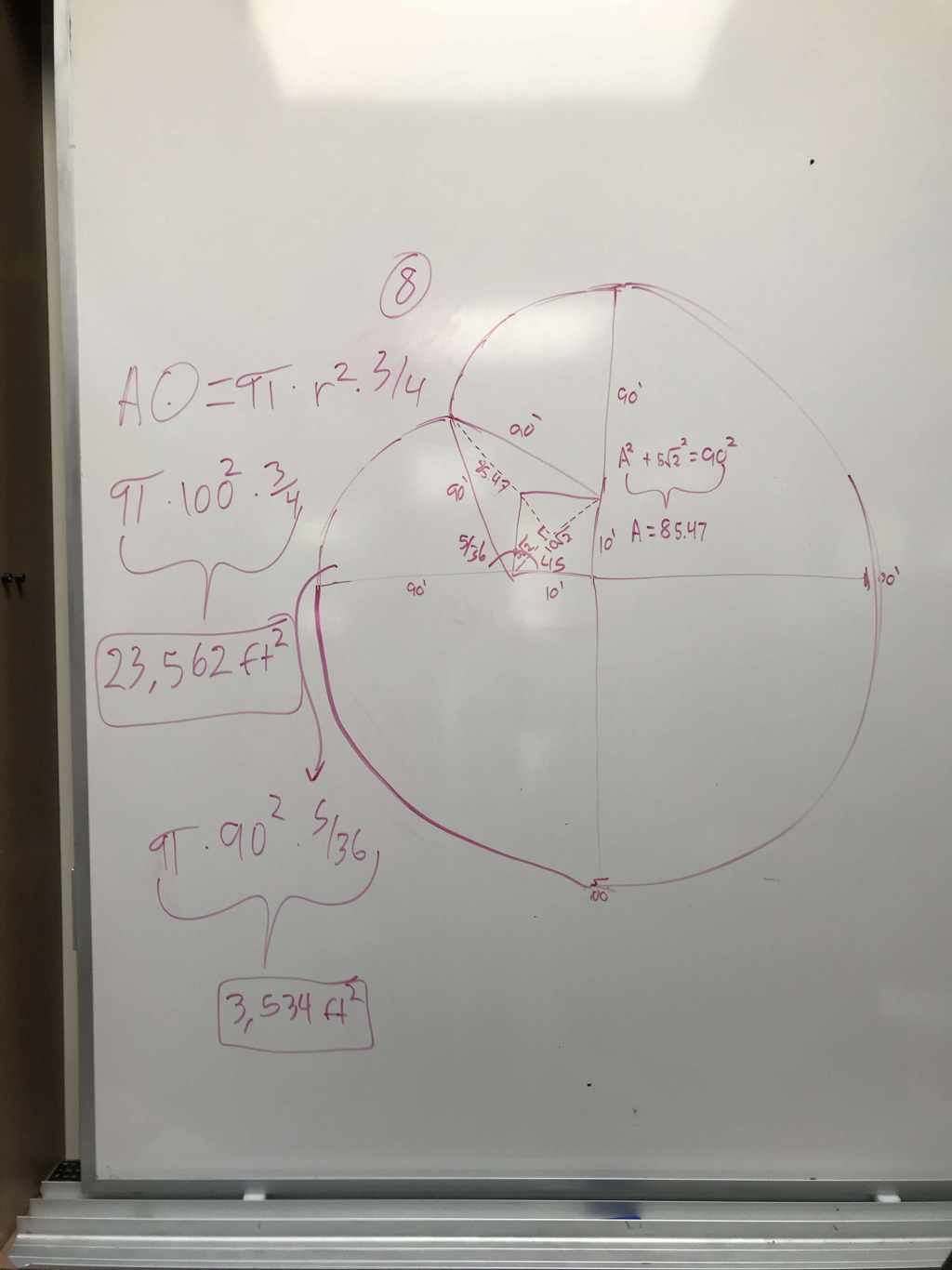
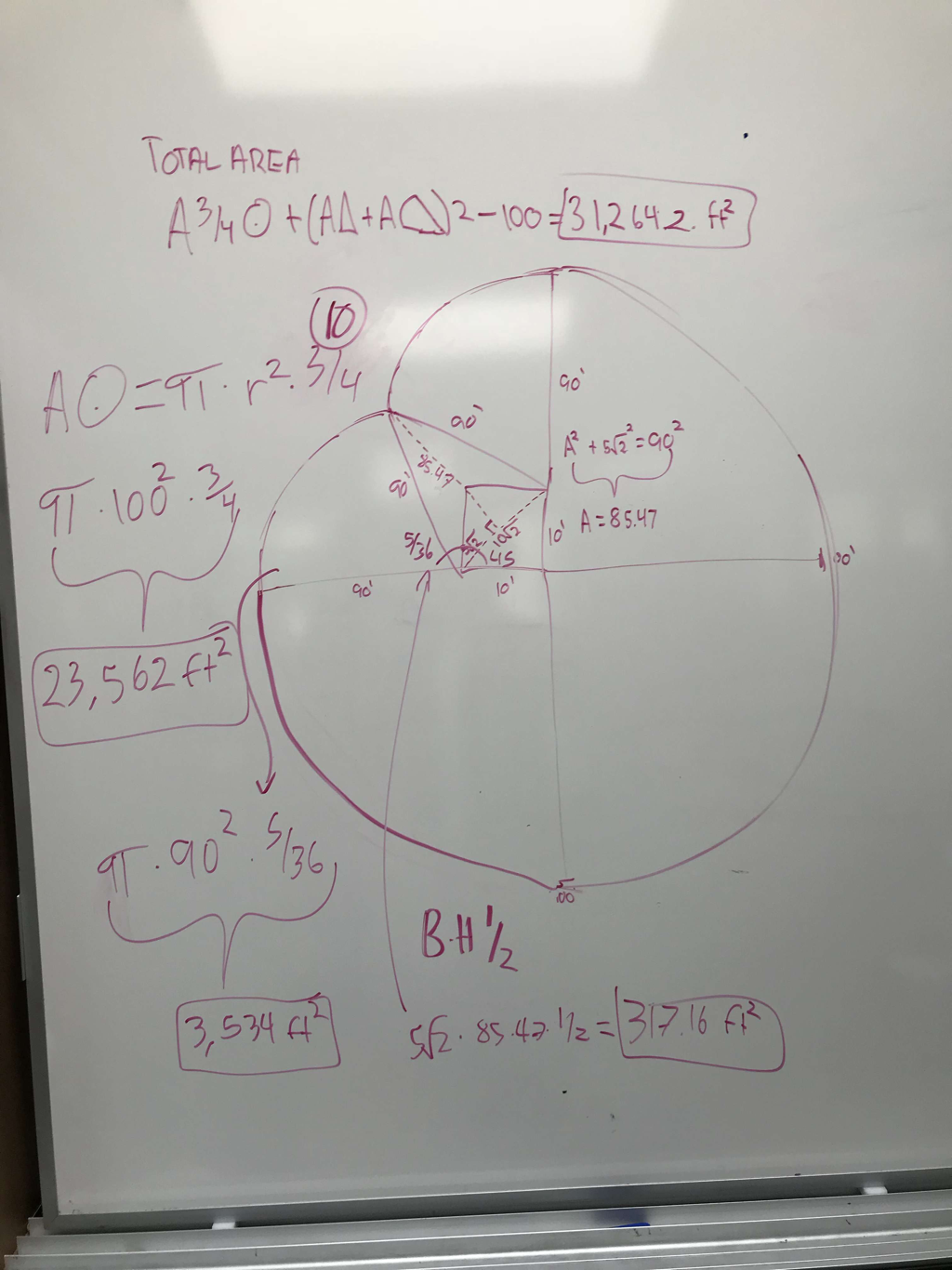
In the cow problem, we had a cow that was tied to a corner of a 10x10 barn, more specifically, the bottom right corner of the barn. The rope that tied the cow to the barn was a 100 ft. long rope. Let's say the cow's name is Bessie and she is trying to see how much land she can graze around her barn while still being tied up. She is a smart cow, so she is going to graze the most land as possible, we just need to figure out how much land that is.
Process
|
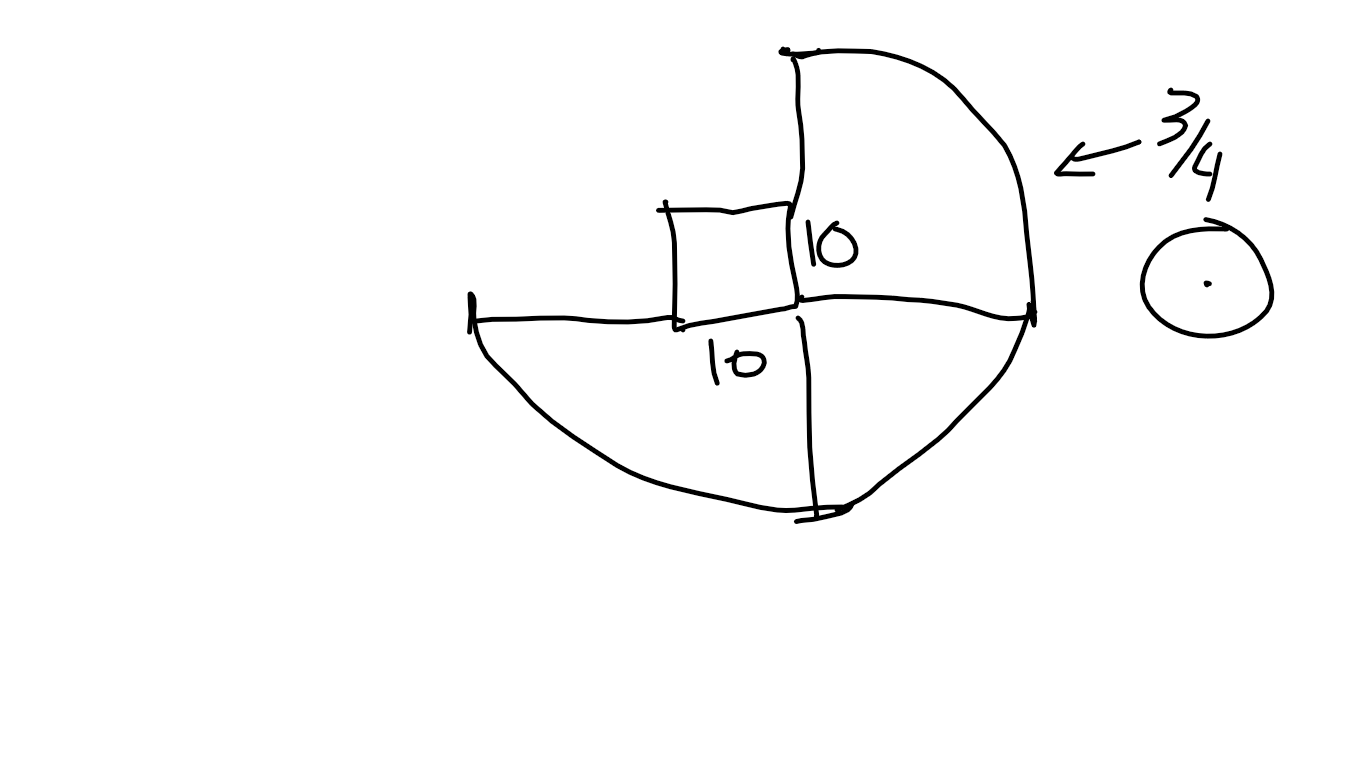
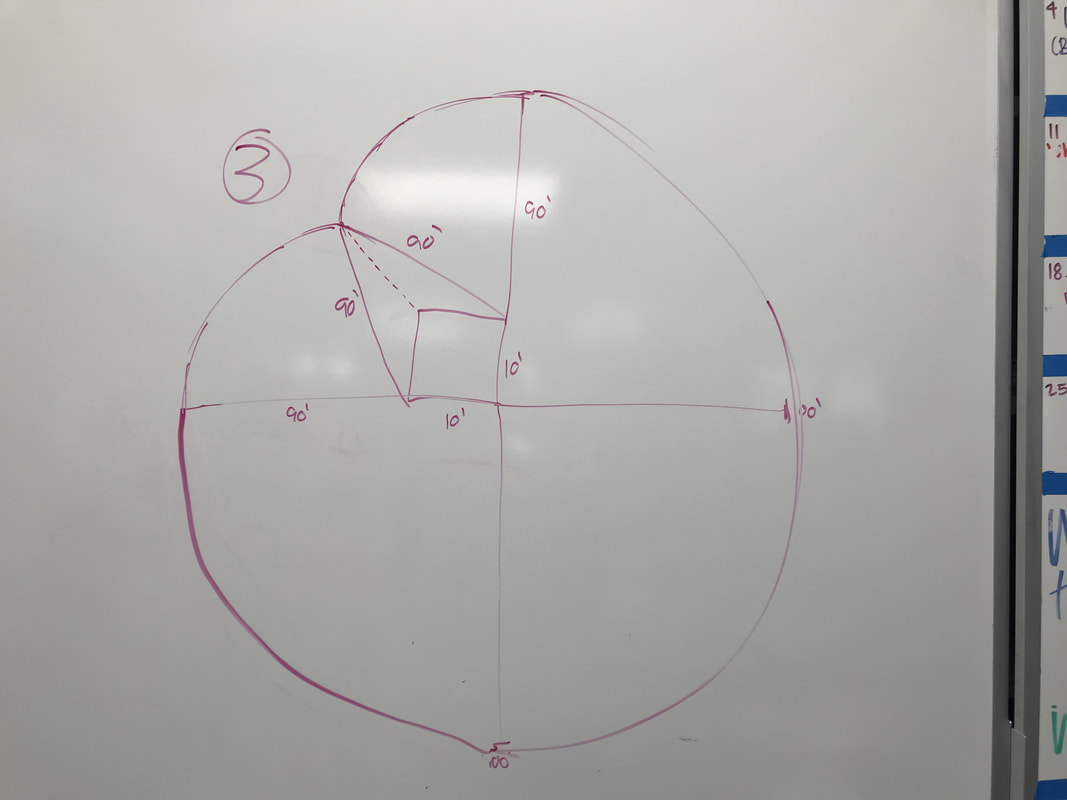
At first, I didn't know much on what to do and I was confused on how to solve the problem. Mr. Carter came in clutch with his knowledge and started to say that Bessie could only graze on 3/4 of the circle. I then continued to draw a 10x10 barn with a 100 ft. rope that could only go 3/4 of a circle around the barn.
|
|
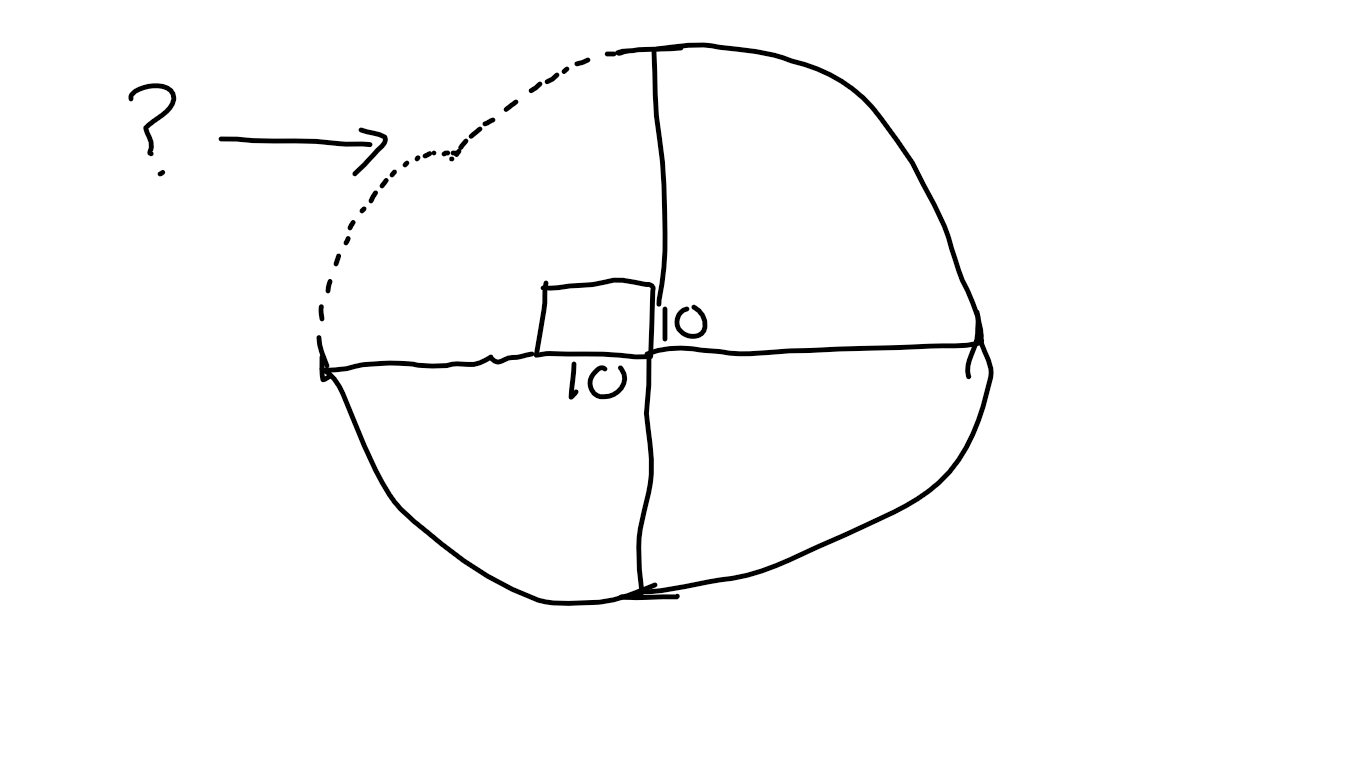
My first attempt was alright taking in the fact that I didn't know much except that I needed a protractor to draw better circles. I tried to make a curve but I didn't know how to accurately because I didn't calculate the loss of rope due to the corner. After that, I did some snooping around other tables and found some very useful equations.
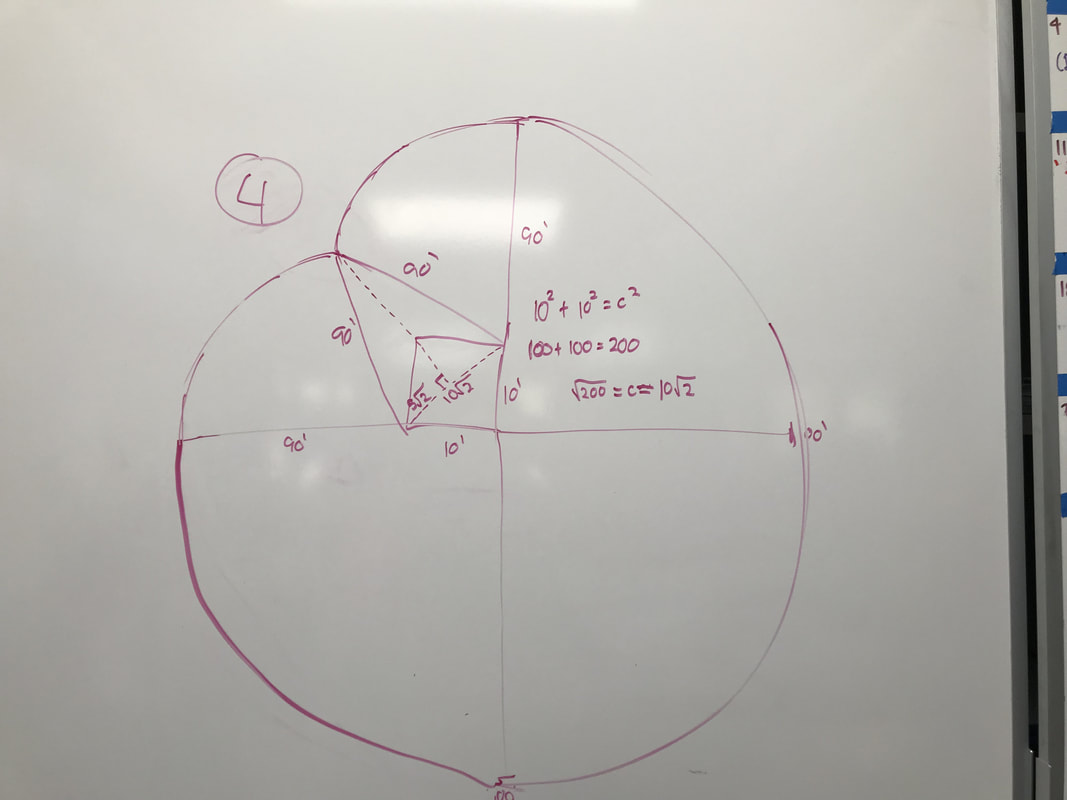
Area of a circle: πr² Area of a triangle: bh 1/2 Area of a square= L x W Phythagorean Theorem: a²+b²=c² SIN: O/H |
|
Breakdown Of Final Solution
|
Step #1
10x10 ft. barn with a 100ft rope |
|
Step #2
Draw out the area that the cow (Bessie) can graze without loss of rope (3/4). Also, the barn plays a role with the 100 ft. rope because Bessie will lose 10 ft. of rope just crossing the barn and have only 90 ft. of rope left. |
|
|
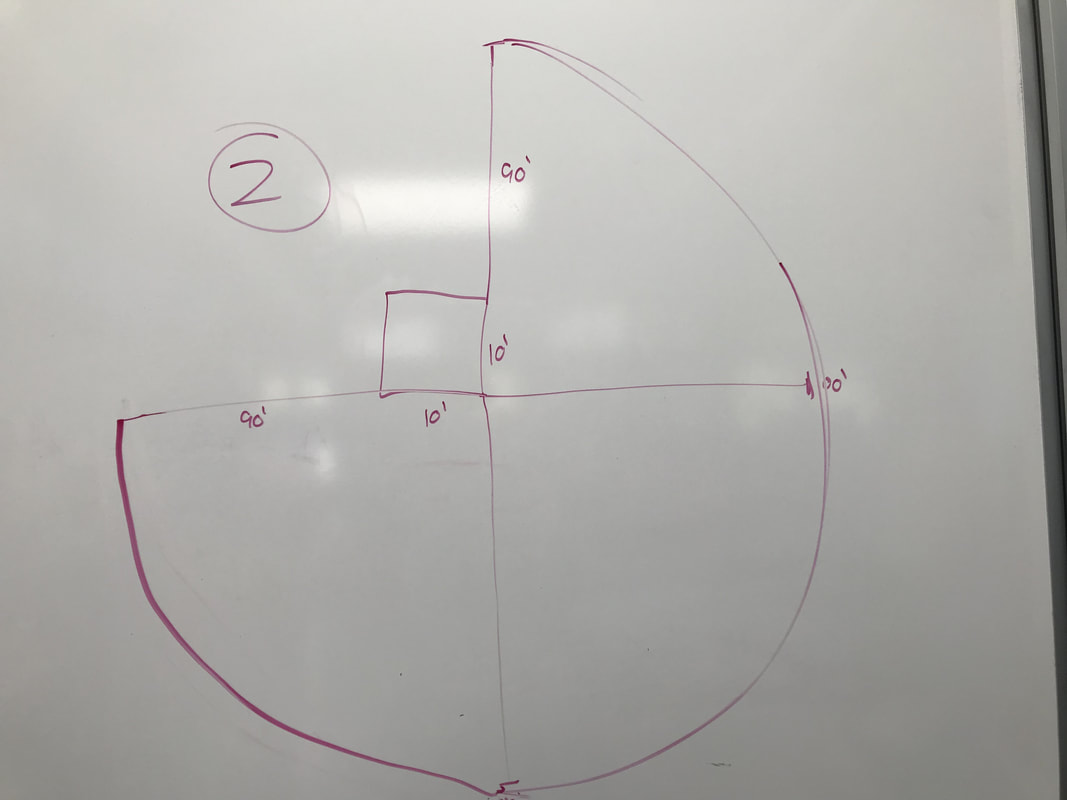
Step #3
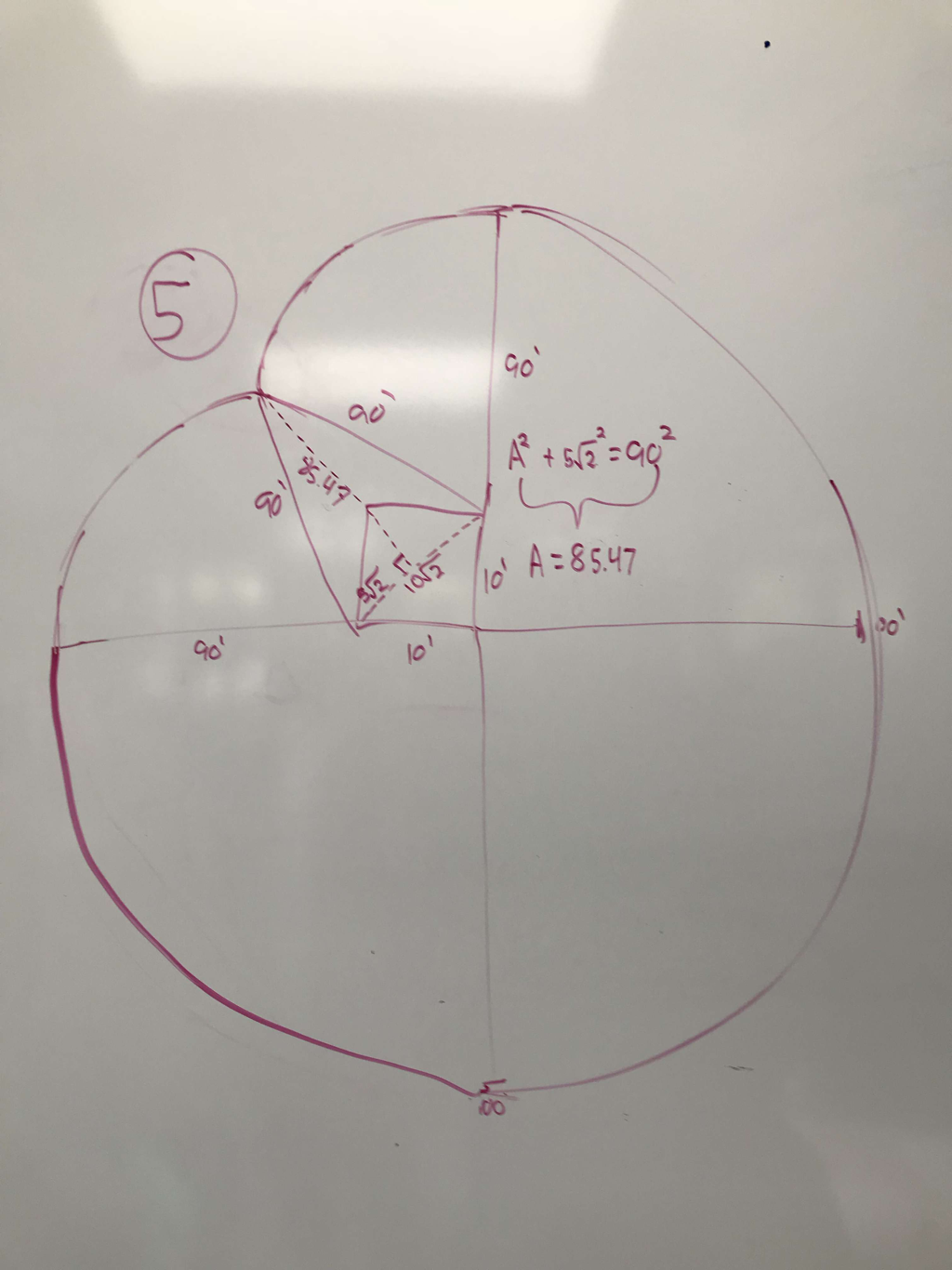
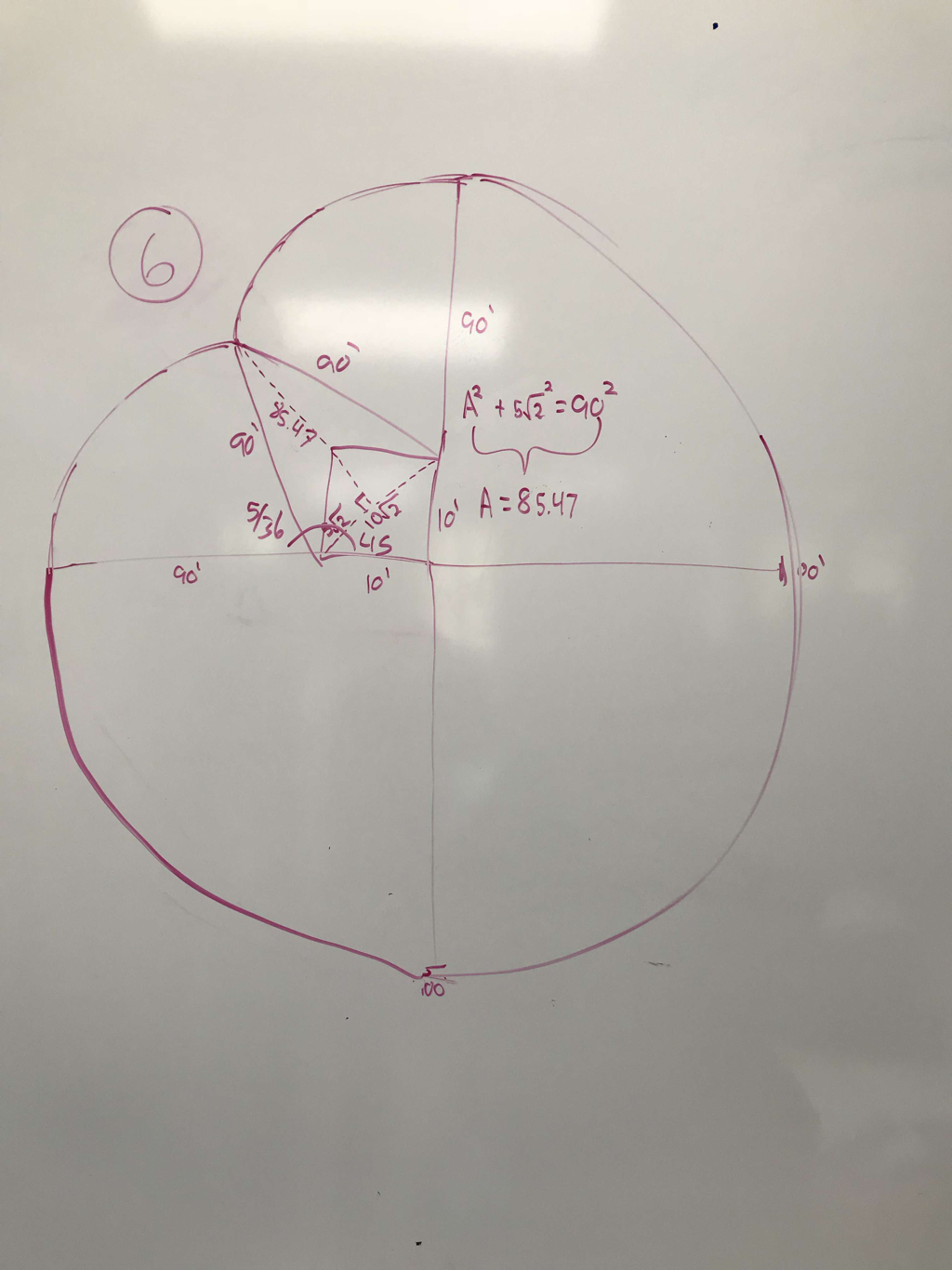
Let's assume Bessie is a smart cow and won't go past the point where the curved lines meet (dimple). Once she reaches that point, if she wants to go eat the grass on the other side, she's going to have to go all the way around. My group also figured out that the length from the bottom left and top right to the "dimple" will be 90 because you're going to lose 10 ft. of rope due to the left and top walls of the barn. We also can't solve for the top left of the circle because we don't know the length of the circles. |
|
Step #4
Now that we have the lengths figured out, we need to use the pythagorean theorem to find the height of the triangle we made. 10^2+10^2=C^2 and all of this simplifies down to 10√2. Now that we have our base, we can solve for the height of the triangle using once again the pythagorean theorem. |
|
|
Step #5
Now that we have our base, we need to split it in half because we want to use the Pythagorean theorem to find the height. |
|
Step #6
Once we have our height, we need to solve for angles to find the angle of the bottom sector of the circle. We did this because you can find the area of a circle as long as you have a portion of it. Example: 300/360 * (pi) * r^2 |
|
|
Step #7
now that we have our angle 5/36, we can start solving the whole problem starting with the 3/4 circle. |
|
Step #8
after we find the area of the 3/4 circle, we can start finding the area of the two sectors. |
|
|
Step #9
Last thing we need to do before we're done is to find the area of the triangle to compete the equation. |
|
Step #10
We used the equation (right) to calculate the total area and we had to subtract 100 because we were cutting into the area of the barn and we only wanted the outside so we found the area of half the barn (100) and subtracted it from our original answer. |
|
Mathematical Equations Used
Area of a circle: πr²
Area of a triangle: bh/2
Area of a square= L x W
Pythagorean Theorem: a²+b²=c²
SOHCAHTOA
Area of a triangle: bh/2
Area of a square= L x W
Pythagorean Theorem: a²+b²=c²
SOHCAHTOA
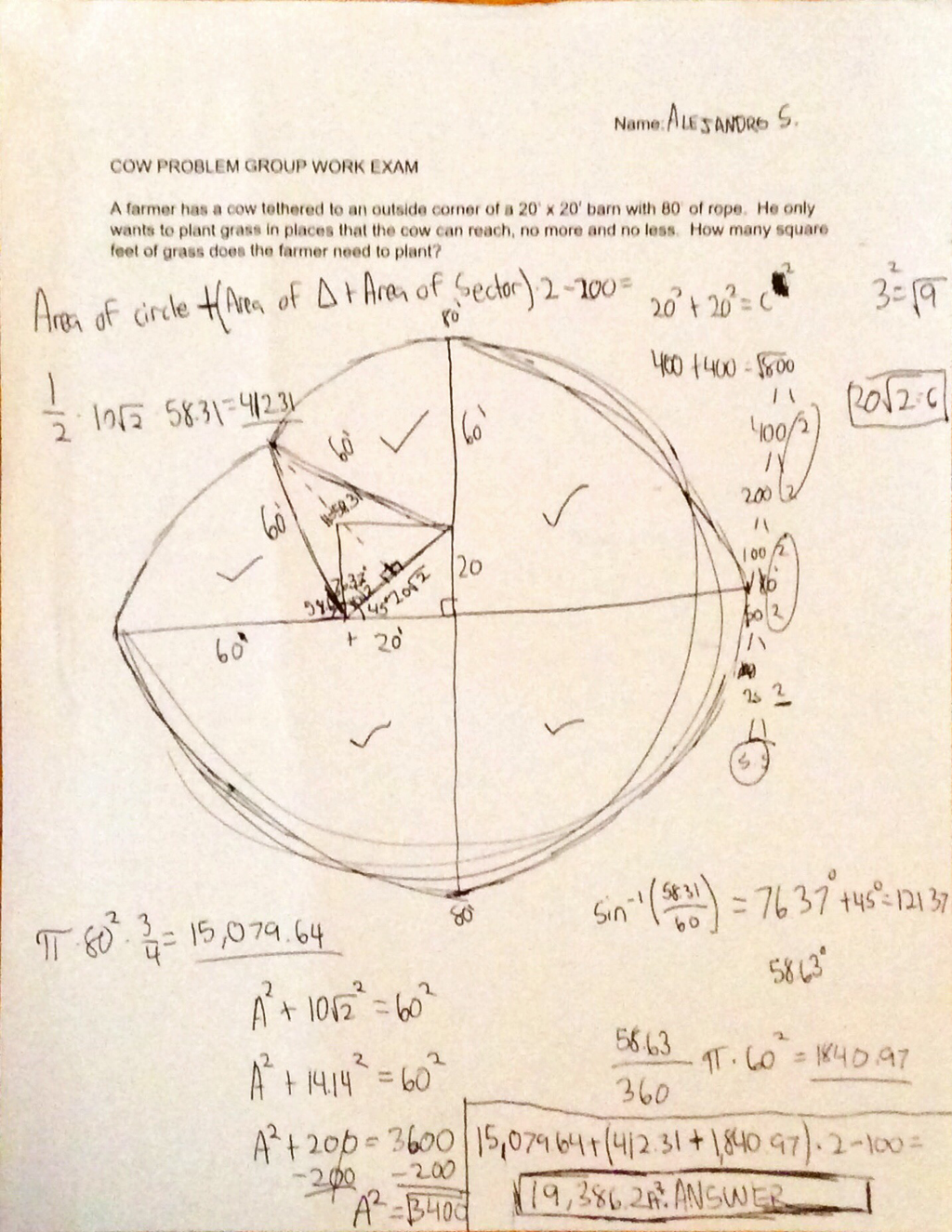
Group Test
|
As you can see, my group and I did good on the group test and got full credit because of our outstanding communication.
|
Individual Test
*I need to have a picture of my individual test but I lost it*
For my individual test, I did alright in my opinion and I got a good score on it. I could’ve done better if I took my time and answered each question with more thought instead of trying to finish fast.
For my individual test, I did alright in my opinion and I got a good score on it. I could’ve done better if I took my time and answered each question with more thought instead of trying to finish fast.
Evaluation/Reflection
This cow Problem really pushed me to remembering all the equations I learned in sophomore year and it did so successfully because mid-solving things, I would remember sohcahtoa or the Pythagorean theorem.
The group quiz was a nice challenge because everyone had to know what to do and by the end, everyone knew how to solve the problem which was a big win for me because I consider myself as a teacher.
If I were asked to grade myself on this unit, I would give myself an A+ because of my efforts to learn and teach other people how to solve the problem. I am a fast learner so I can retain information for a long time and teach it if I know everything 100%. I contributed a lot to my group and that felt nice because there were a lot of “OHHHHHH”s when I was explaining stuff. So overall, I liked this problem and it felt nice to connect with my group.
The group quiz was a nice challenge because everyone had to know what to do and by the end, everyone knew how to solve the problem which was a big win for me because I consider myself as a teacher.
If I were asked to grade myself on this unit, I would give myself an A+ because of my efforts to learn and teach other people how to solve the problem. I am a fast learner so I can retain information for a long time and teach it if I know everything 100%. I contributed a lot to my group and that felt nice because there were a lot of “OHHHHHH”s when I was explaining stuff. So overall, I liked this problem and it felt nice to connect with my group.
