Problem Statement

My group started off this problem by measuring the height of a person and then stacking them on top of each other and finding the height of the flagpole. When you first arrive at HTHCV, the first thing thing that will catch your eye will be the tall flagpole. So my group and I took on the task of using the three methods Mr.Ginsberg showed us, shadow method, isosceles triangle method, and mirror method, and saw what we can accomplish. 
The questions we took on with this problem were:
What was your initial guess for the height of the flagpole before we took any measurements?
What was your estimation using the shadow method?
What was your estimation using the mirror method?
What was your estimation using the isosceles triangle method?

Process and Solution

The first thing we did as a group was to go outside and look at the flagpole to see how high it could be. What my group came up with was to stand next to the flagpole and imagine how many "of them" we could stack on top of each other to reach the top. My initial guess was 55 feet and my maximum was 80 feet. Mr.Ginsberg told us that the whole problem was revolving around similarity. Similarity is when two shapes have equal ratios and they have corresponding sides.

Shadow Method

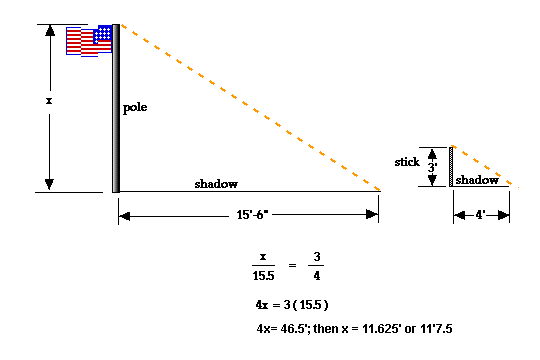
The very first method my group got showed was the shadow method. To use the shadow method, you get the object you want to measure the height of and measure its shadow. Once you measure that shadow, you get another object and make it so their shadow is exactly where the shadow of the taller object casts it shadow. We can use the known height of the one object to find the height of the unknown one. This makes it so we can find the equivalent ratio. You can form two similar triangles for this method. You can see how (below) the smaller triangle is similar to the larger triangle. After you got the height of the smaller object, you can plug it into an equation to find the height (below). My group and I took my height because I was the tallest in the group and then got the flagpole's height by using the shadow method.  After doing all the work, we ended with the estimated height of the flagpole to be 53.1 feet. 

Mirror Method

The second measurement that Mr. Ginsberg showed us was the mirror method. What you do is place a mirror down on the ground and stare at it until you see the top of object you want to know the height of. After you see the top of the other object, you measure the distance from you and the mirror. You also measure the distance between the mirror and the object you want to know the height of. After that, you take your height and the distance to the mirror and you have a fraction you can work with (Look at fraction on top). My group and I did this with a basketball hoop and got 10.11 feet.

Isosceles Method

All Isosceles triangles have two same sides and two same angles. Mr. Ginsberg taught us this because we can use isosceles triangles like similar triangles and find the ratios or height. The method we used:

We took the flagpole and it's shadow and turned it into an isosceles triangle by labeling the flagpole and its shadow ABC. Then, a person's shadow should match up with the top of the flagpole's shadow. The top of the flagpole shadow is matched with the top of my shadow (head). With this you get the length of your shadow and the length of the flagpole's shadow and see the ratio between your height and your shadow and use the scale factor to multiply against the flagpole's shadow height.

Problem Evaluation

These problems really pushed me into trying out new ways to find heights of object using various methods. Although it was hard at first, Mr. Ginsberg was really helpful to us and showed us ways we didn't even know how to do. I learned how to be patient and getting people to understand me better whenever I'm explaining something to them. Great work!

Self Evaluation

I deserve an A+ for this unit because I felt like I really pushed myself into thinking new ways of finding heights and also because I helped a lot of people out. All this hard work got me a 16/18 on the quiz Mr.Ginsberg gave us and I am really proud of myself for getting that grade.

Edits

My critiquer Jonah, told me to explain more in the shadow method and also to change the font size because it was too big on mobile devices. 
Jonah's awesome DP is down below.